Magnitude Scaling

Magnitude Scaling#

import warnings

import IPython.display as ipd
import matplotlib.pyplot as plt
import librosa.display
import numpy

from mirdotcom import mirdotcom

warnings.filterwarnings("ignore")
mirdotcom.init()

Often, the raw amplitude of a signal in the time- or frequency-domain is not as perceptually relevant to humans as the amplitude converted into other units, e.g. using a logarithmic scale.

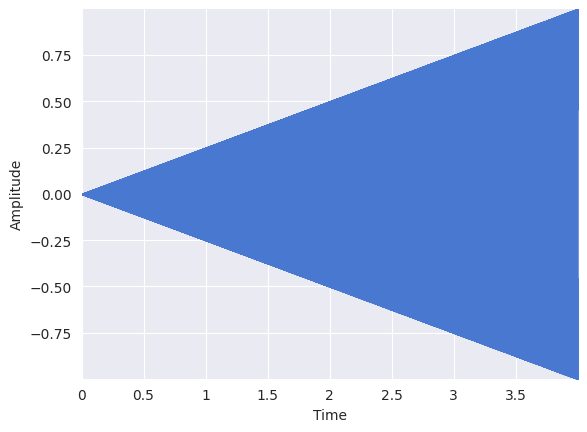
For example, let’s consider a pure tone whose amplitude grows louder linearly. Define the time variable:

T = 4.0  # duration in seconds
sr = 22050  # sampling rate in Hertz
t = numpy.linspace(0, T, int(T * sr), endpoint=False)

Create a signal whose amplitude grows linearly:

amplitude = numpy.linspace(0, 1, int(T * sr), endpoint=False)  # time-varying amplitude
x = amplitude * numpy.sin(2 * numpy.pi * 440 * t)

Listen:

ipd.Audio(x, rate=sr)

Plot the signal:

librosa.display.waveshow(x, sr=sr)
plt.ylabel("Amplitude")

Text(22.472222222222214, 0.5, 'Amplitude')
../../_images/43dde28ff133e7164eba7e6ee5b599cc0d0a5b9e7ac28c8bcc55ec7fdb26e0a0.png

Now consider a signal whose amplitude grows exponentially, i.e. the logarithm of the amplitude is linear:

amplitude = numpy.logspace(-2, 0, int(T * sr), endpoint=False, base=10.0)
x = amplitude * numpy.sin(2 * numpy.pi * 440 * t)

ipd.Audio(x, rate=sr)

librosa.display.waveshow(x, sr=sr)
plt.ylabel("Amplitude")

Text(22.472222222222214, 0.5, 'Amplitude')
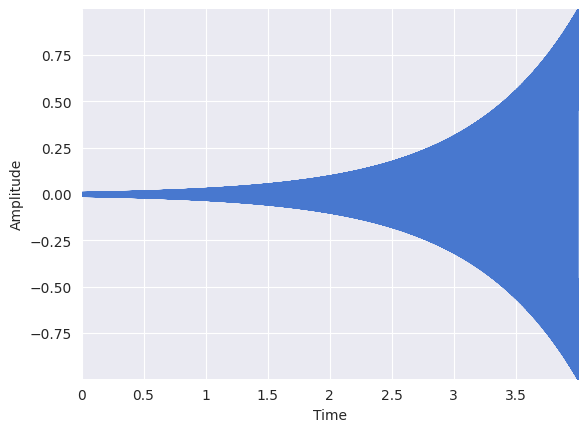
../../_images/71f38be9c21a0473c220357ab9958ada2eaac7a1f5a2ebe0bc8faebd92a7dfb9.png

Even though the amplitude grows exponentially, to us, the increase in loudness seems more gradual. This phenomenon is an example of the Weber-Fechner law (Wikipedia) which states that the relationship between a stimulus and human perception is logarithmic.

Spectrogram Visualization: Linear Amplitude#

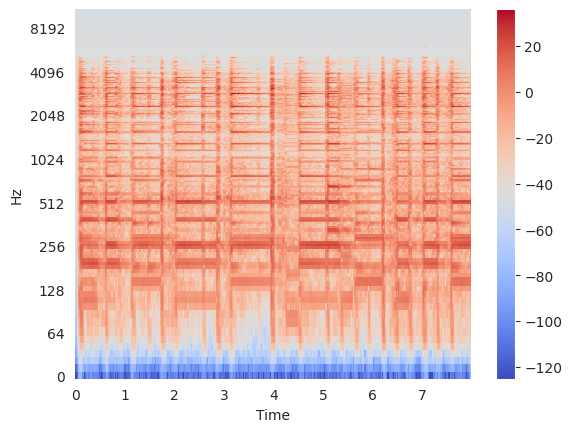
Let’s plot a magnitude spectrogram where the colorbar is a linear function of the spectrogram values, i.e. just plot the raw values.

fp = mirdotcom.get_audio("latin_groove.mp3")
x, sr = librosa.load(fp, duration=8)
ipd.Audio(x, rate=sr)

X = librosa.stft(x)
X.shape

(1025, 345)

Raw amplitude:

Xmag = abs(X)
librosa.display.specshow(Xmag, sr=sr, x_axis="time", y_axis="log")
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7091ad41ad10>
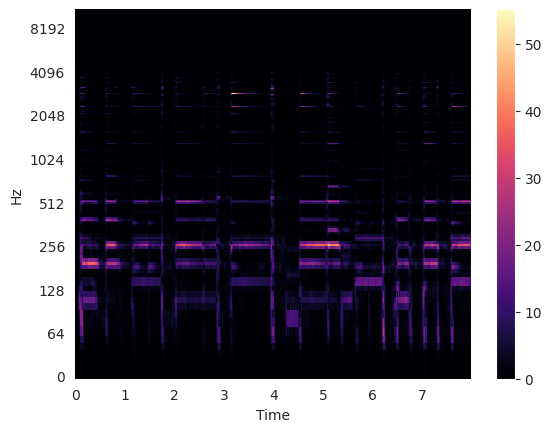
../../_images/94e26041aa812bc980432d6d2ef782520eb8a9de5e33a41bf90283672b05935a.png

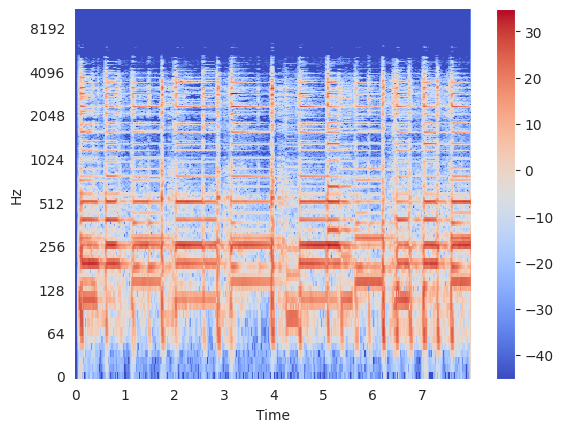
Spectrogram Visualization: Log Amplitude#

Now let’s plot a magnitude spectrogram where the colorbar is a logarithmic function of the spectrogram values.

Decibel (Wikipedia)

librosa.amplitude_to_db:

Xdb = librosa.amplitude_to_db(Xmag)
librosa.display.specshow(Xdb, sr=sr, x_axis="time", y_axis="log")
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7091ad312950>
../../_images/3e523ac849008ebe8a32c3222c52232b0ddd8e28bb7fa3440964a5daa1de26c1.png

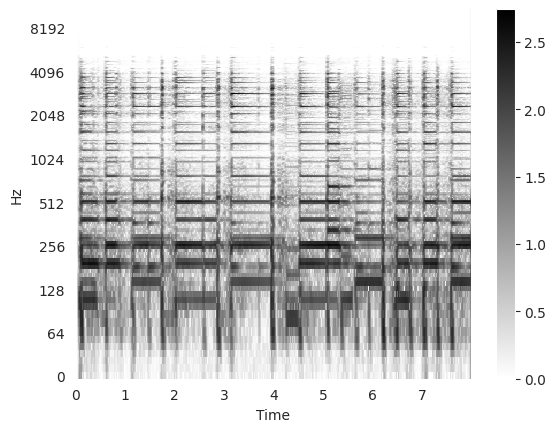
One common variant is the \(\log (1 + \lambda x)\) function, sometimes known as logarithmic compression (FMP, p. 125). This function operates like \(y = \lambda x\) when \(\lambda x\) is small, but it operates like \(y = \log \lambda x\) when \(\lambda x\) is large.

Xmag = numpy.log10(1 + 10 * abs(X))
librosa.display.specshow(Xmag, sr=sr, x_axis="time", y_axis="log", cmap="gray_r")
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7091ad2241f0>
../../_images/2f8d690d35a86701a7361ff4d2309feac48936279ffc3db9932ac43cfe5c336c.png

Spectrogram Visualization: Perceptual Weighting#

librosa.perceptual_weighting:

freqs = librosa.core.fft_frequencies(sr=sr)

Xmag = librosa.perceptual_weighting(abs(X) ** 2, freqs)
librosa.display.specshow(Xmag, sr=sr, x_axis="time", y_axis="log")
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x7091ad1060b0>
../../_images/600208e416ff2dec054f4093f2bb0115fe6f6ff66cf4e996c429cf59a755158b.png
Contents