Nonnegative Matrix Factorization

Nonnegative Matrix Factorization#

import warnings

import IPython.display as ipd
import matplotlib.pyplot as plt
import librosa.display
import numpy

from mirdotcom import mirdotcom

warnings.simplefilter("ignore")
mirdotcom.init()

Nonnegative matrix factorization (NMF) is an algorithm that factorizes a nonnegative matrix, \(X\), into a product of two nonnegative matrices, \(W\) and \(H\). It is an unsupervised iterative algorithm that minimizes a distance between \(X\) and the product \(WH\):

\[ \min_{W, H} d(X, WH) \]

If \(X\) has dimensions \(M\) by \(N\), then \(W\) will have dimensions \(M\) by \(R\), and \(H\) will have dimensions \(R\) by \(N\), where inner dimension \(R\) is the rank or number of components of the decomposition.

When applied to a musical signal, we find that NMF can decompose the signal into separate note events. Therefore, NMF is quite useful and popular for tasks such as transcription and source separation.

The input, \(X\), is often a magnitude spectrogram. In such a case, we find that the columns of \(W\) represent spectra of note events, and the rows of \(H\) represent temporal envelopes of the same note events.

Let’s load a signal:

filename = mirdotcom.get_audio("conga_groove.wav")
x, sr = librosa.load(filename)

ipd.Audio(x, rate=sr)

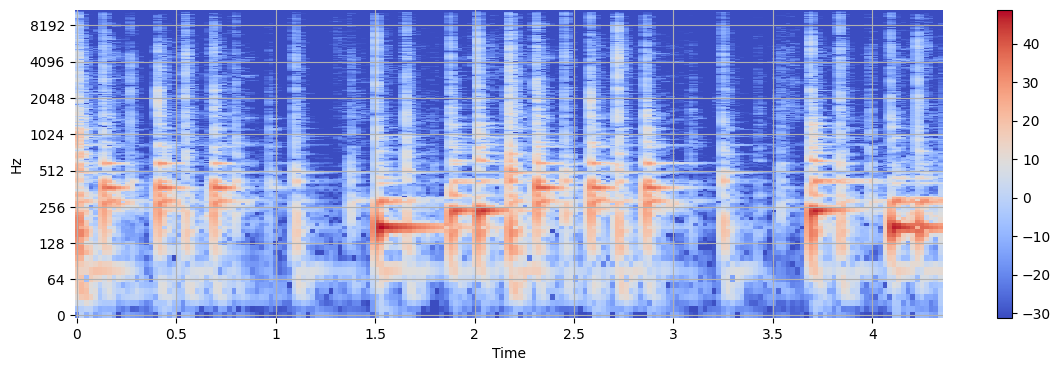
Compute the STFT:

S = librosa.stft(x)

S_db = librosa.amplitude_to_db(abs(S))
plt.figure(figsize=(14, 4))
librosa.display.specshow(S_db, sr=sr, x_axis="time", y_axis="log")
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x78291b0f19f0>
../../_images/29c0b071460f0641cea37e84aa979527045c00a9a38788255b11d0ee908974ab.png

Factorizing in Python#

We will use librosa.decompose.decompose to perform our factorization. librosa uses sklearn.decomposition.NMF by default as its factorization method.

X, X_phase = librosa.magphase(S)
n_components = 6
W, H = librosa.decompose.decompose(X, n_components=n_components, sort=True)

print(W.shape)
print(H.shape)

(1025, 6)
(6, 188)

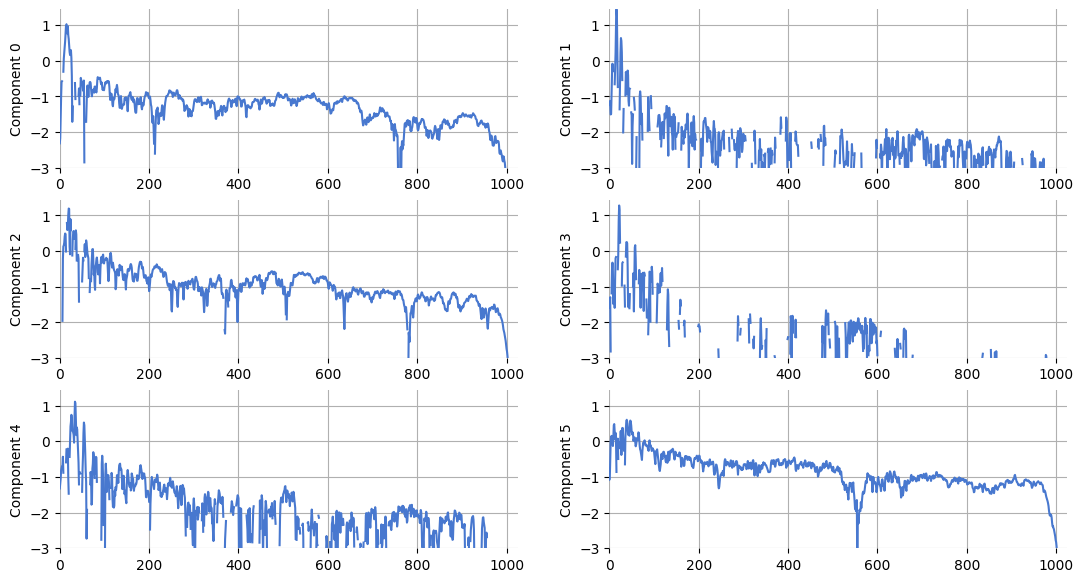
Let’s display the spectral profiles, \(\{w_1, ..., w_R\}\):

plt.figure(figsize=(13, 7))
logW = numpy.log10(W)
for n in range(n_components):
    plt.subplot(int(numpy.ceil(n_components / 2.0)), 2, n + 1)
    plt.plot(logW[:, n])
    plt.ylim(-3, logW.max())
    plt.xlim(0, W.shape[0])
    plt.ylabel("Component %d" % n)
../../_images/739d5dcb0736b6aca7c8976083382ec2795c53a65d9f97ca1c3276aa043a3a7e.png

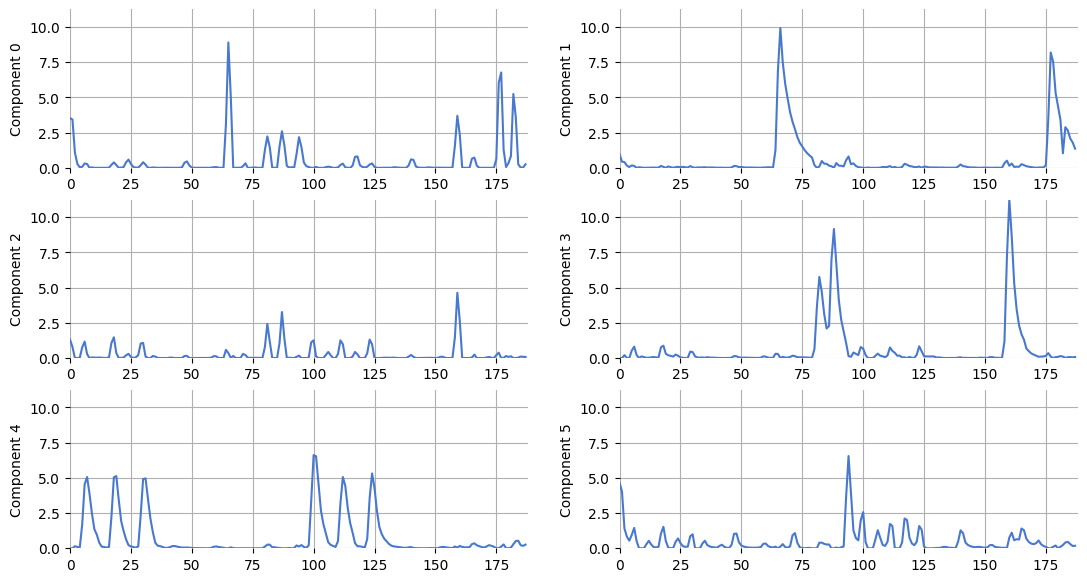
Let’s display the temporal activations, \(\{h_1, ..., h_R\}\):

plt.figure(figsize=(13, 7))
for n in range(n_components):
    plt.subplot(int(numpy.ceil(n_components / 2.0)), 2, n + 1)
    plt.plot(H[n])
    plt.ylim(0, H.max())
    plt.xlim(0, H.shape[1])
    plt.ylabel("Component %d" % n)
../../_images/a08f4f5826f7209521a7e10c8dbfb606f805968a6a9d2eb7ee23e74353e405e7.png

Finally, re-create the individual components, and listen to them. To do this, we will reconstruct the magnitude spectrogram from the NMF outputs and use the phase spectrogram from the original signal.

for n in range(n_components):

    # Re-create the STFT of a single NMF component.
    Y = numpy.outer(W[:, n], H[n]) * X_phase

    # Transform the STFT into the time domain.
    y = librosa.istft(Y)

    print("Component {}:".format(n))
    ipd.display(ipd.Audio(y, rate=sr))

Component 0:

Component 1:

Component 2:

Component 3:

Component 4:

Component 5:

Listen to the reconstructed full mix:

# Re-create the STFT from all NMF components.
Y = numpy.dot(W, H) * X_phase

# Transform the STFT into the time domain.
reconstructed_signal = librosa.istft(Y, length=len(x))
ipd.Audio(reconstructed_signal, rate=sr)

Listen to the residual:

residual = x - reconstructed_signal
residual[0] = 1  # hack to prevent automatic gain scaling
ipd.Audio(residual, rate=sr)

For Further Exploration#

Use different audio files.

Alter the rank of the decomposition, n_components. What happens when n_components is too large? too small?

NMF is a useful preprocessor for MIR tasks such as music transcription. Using the steps above, build your own simple transcription system that returns a sequence of note events, [(onset time, class label, volume/gain)...].

Contents